Games101-2-变换
Games101-2-变换, 对应Games101第三、四节课
Games101现代计算机图形学入门-3
线性变换
缩放
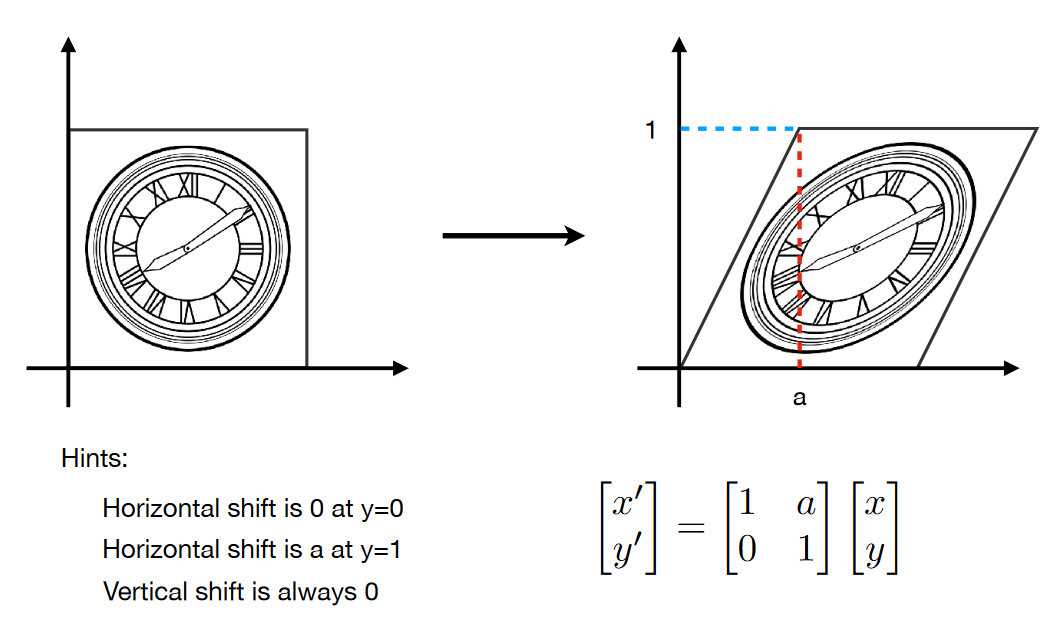
切变
旋转
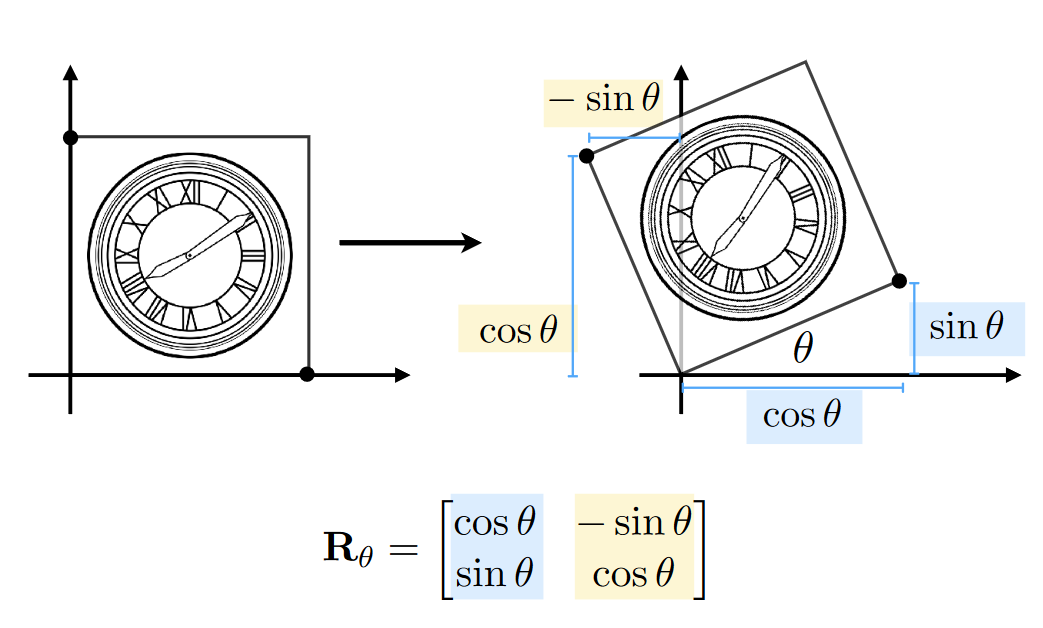
旋转-a角度的矩阵就是旋转a角度的转置矩阵,也是逆矩阵
仿射变换(齐次坐标)
为了解决平移变换不能简单写成矩阵相乘 x’= Mx

向量具有平移不变性,因此向量最后是0

在齐次坐标下,点+点表示这两点的中点

逆变换对应逆矩阵
变换的组合

三维变换

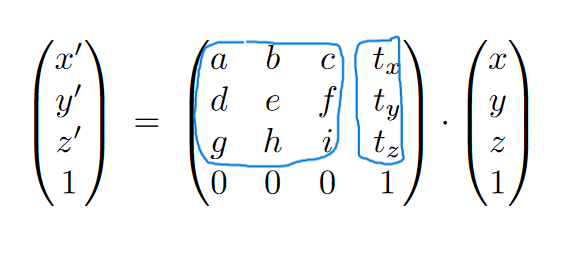
对这种矩阵来说,是先线性变换后仿射变换
三维旋转
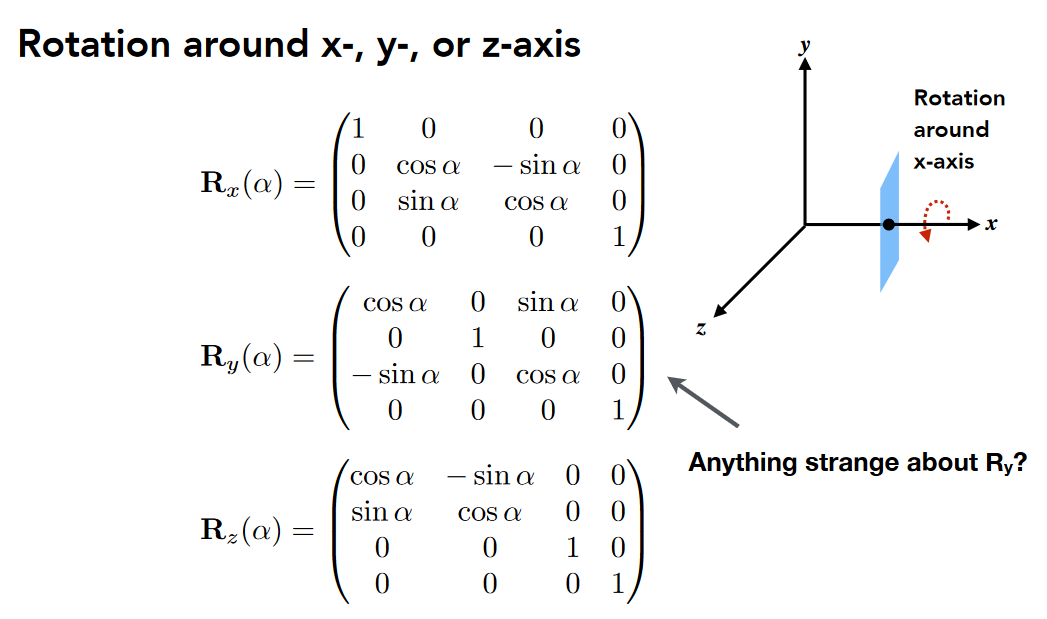
基于右手螺旋定则,y由z叉乘x得到,固正好相反
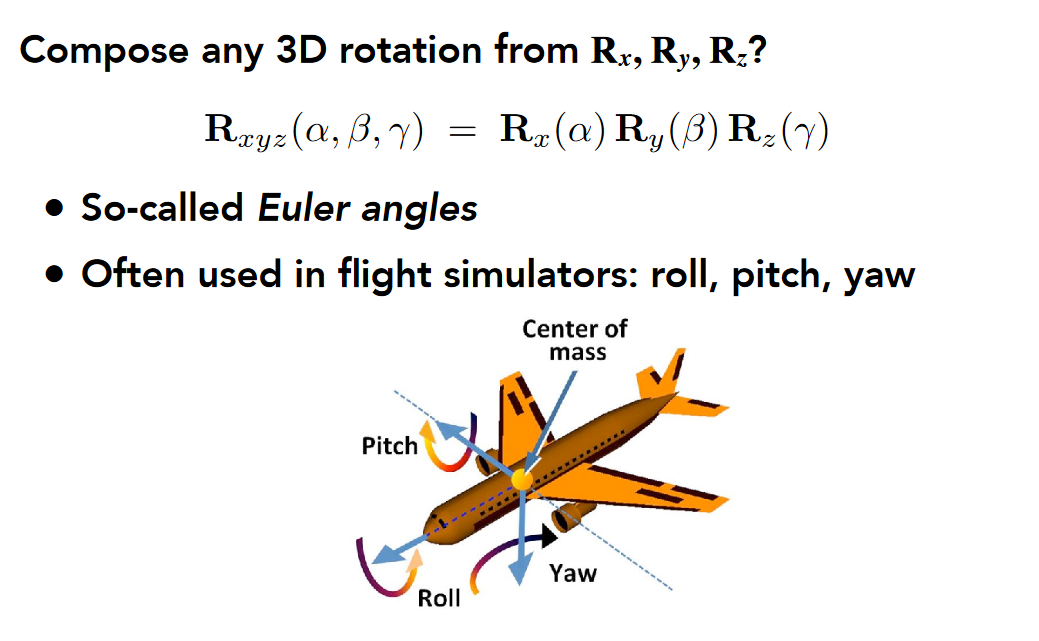
罗格里德斯旋转公式

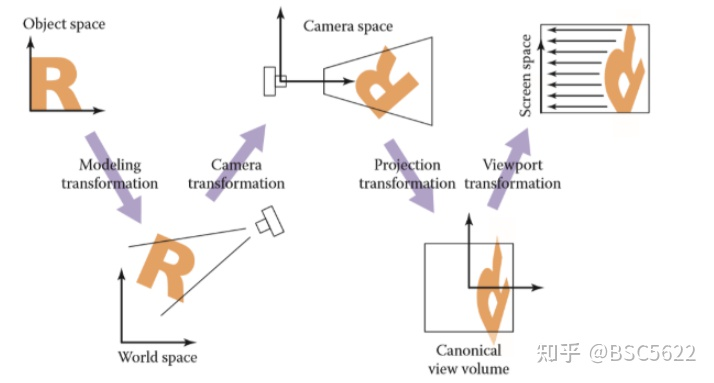
视图变换
确定相机位置
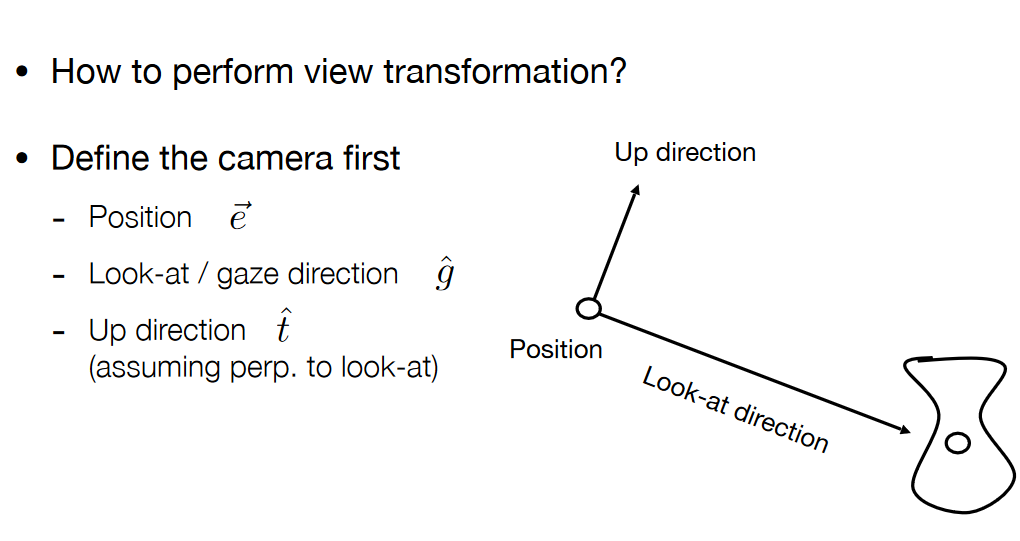

将任意向量旋转到标准轴困难,故做逆操作,将标准轴转到任意向量,之后对旋转矩阵做逆变换,恰好旋转矩阵是正交矩阵,其逆矩阵就是转置矩阵。
投影变换
正交投影
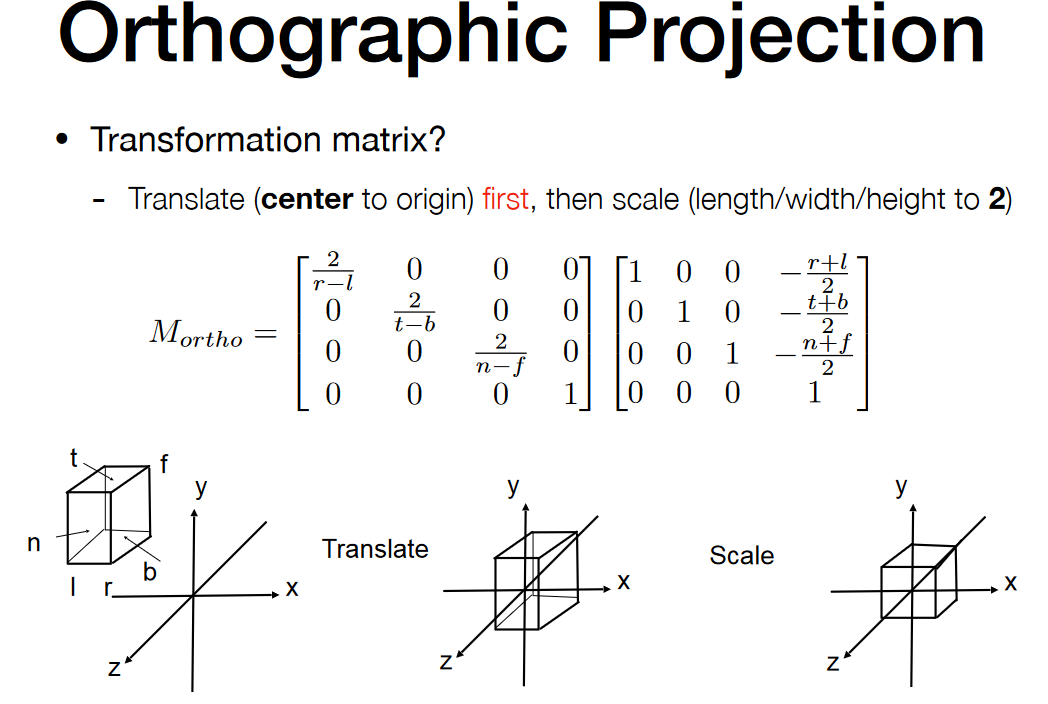
透视投影
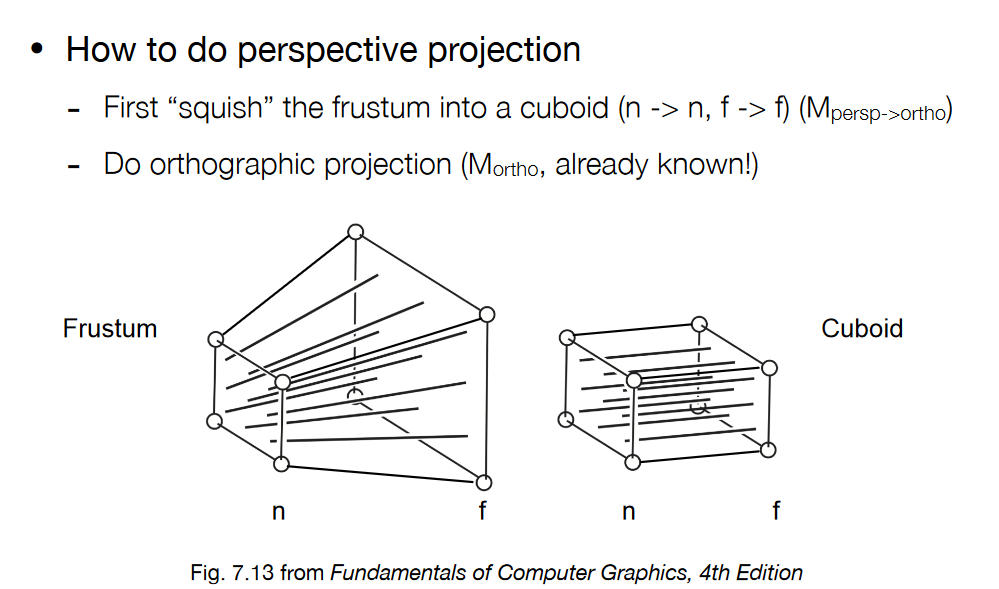
推导思路:先将Frustum挤压成一个长方体,之后再做一次正交投影
推导过程:

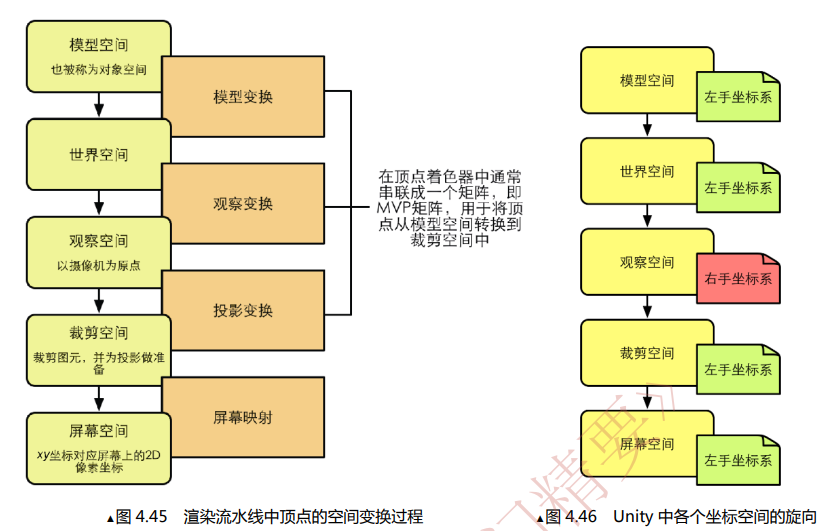
在unity等游戏引擎中,需要在做完投影矩阵变换之后再进行 透视除法,才能将顶点变换到 归一化设备坐标 NDC(Normalized Device Coordinates) 。而在数学中点(x, y, z, w)和(x/w, y/w, z/w, 1)是完全一样的,我们也就认为进行完投影变换后,变换就结束了。
在实际计算中点(x, y, z, w)和(x/w, y/w, z/w, 1)虽然只是写法不同,但是会影响后续计算,所以需要将所有的(x, y, z, w)进行归一化变为(x/w, y/w, z/w, 1),这一步操作叫做 透视除法,在渲染流水线中在顶点着色器输出之后进行。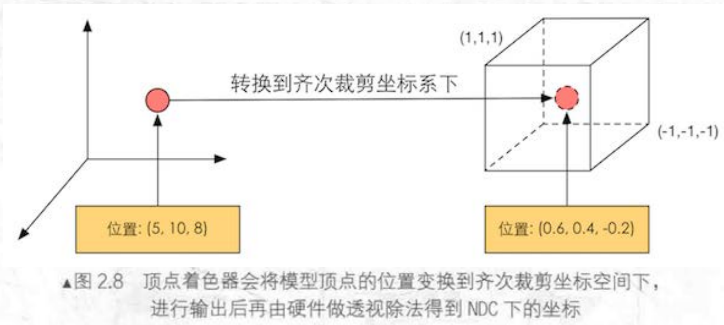
视锥
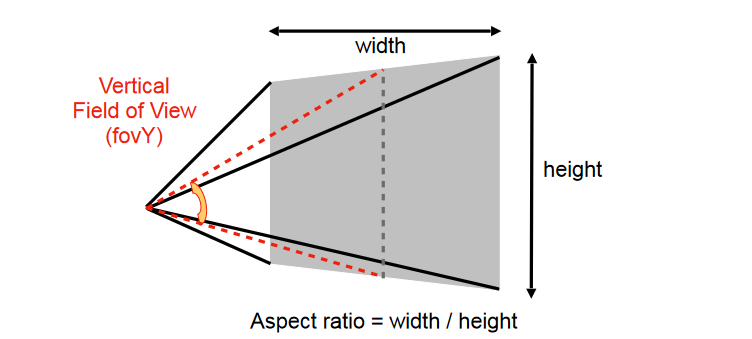
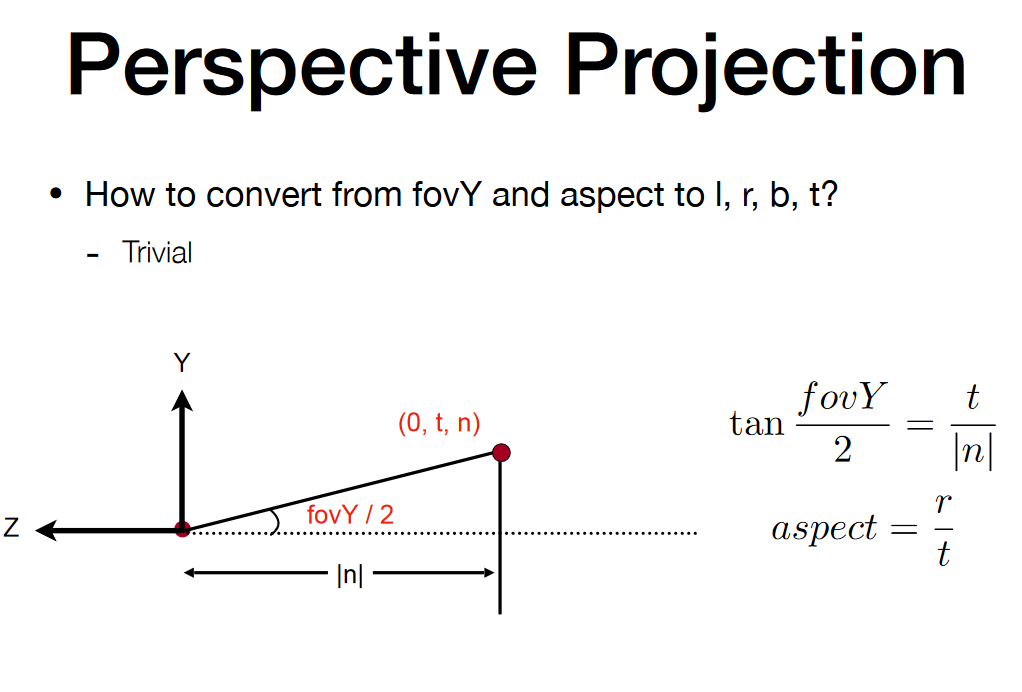
- aspect ratio: 宽高比(观测角度)
- Field of View(fovY): 可视角度
总结
homework0
代码
1 | |
重点关注点,向量和矩阵定义的方法
homework1
代码
1 | |
运行结果: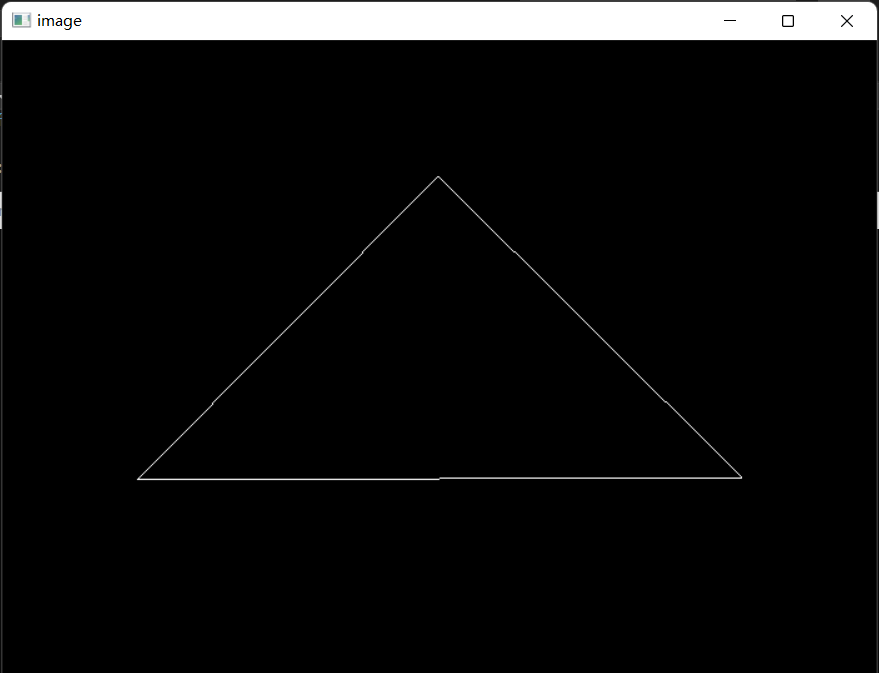
注意:
- 角度要进行转换
- 一开始绘制的三角形是倒着的,是因为默认zNear和zFar是正值,但实际上其均为负值,故对其取负值。
参考
Games101-2-变换
https://kenny-hoho.github.io/2022/07/21/Games101-2-变换/