万向节死锁问题（Gimbal Lock）

在Game104的动画章节中，讲解了欧拉角存在的问题，其中最难理解的就是欧拉角的万向节死锁问题，特此记录一下对这个问题的理解。

参考资料：
bilibili_无伤理解欧拉角中的“万向死锁”现象

欧拉角（Euler Angle）

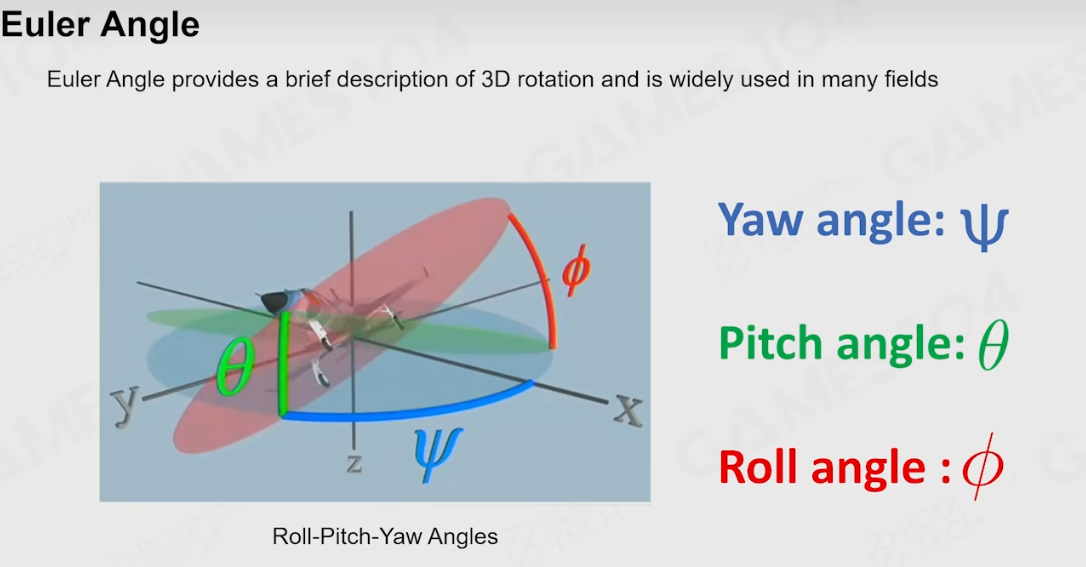
欧拉证明了三维空间内的任意旋转，可以由围绕三个正交轴旋转组合而来。如上图所示，旋转用旋转矩阵表示，将围绕三个轴的旋转矩阵相乘即可得到实现任意旋转的旋转矩阵。

万向节死锁（Gimbal Lock）

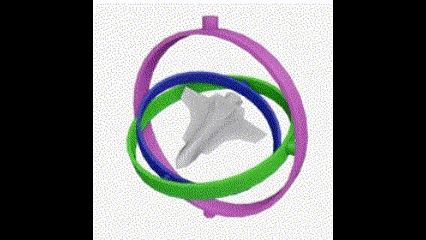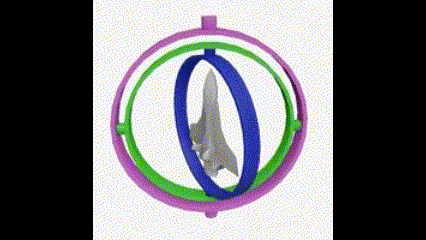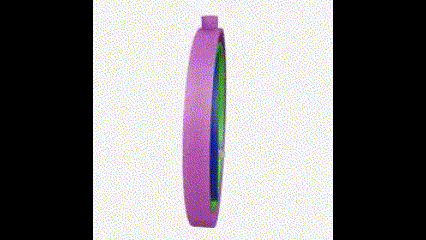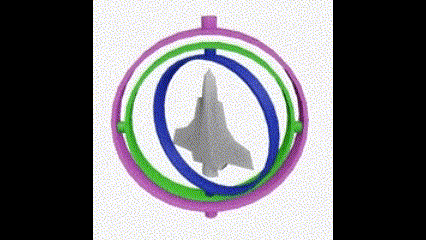
一般用上图中的平衡环解释什么是万向节死锁。在平衡环案例中可以轻易看出万向节死锁发生的原理，两个环重叠在同一个平面，导致最外圈的大环旋转和最内圈的小环旋转的结果完全一样，都是绕竖直方向旋转。

产生这个现象有一个前提条件，即外圈环的旋转会带动内圈环的旋转，而内圈环的旋转不能带动外圈环的旋转。用坐标系来理解：我们规定一个旋转变换的顺序，按照绕X轴Y轴Z轴的顺序将三个旋转矩阵相乘得到最终旋转矩阵，绕X轴的旋转会带动Y轴和Z轴的旋转，Y轴的旋转只能带动Z轴的旋转，这就导致如果我们绕Y轴旋转90°，Y轴会带动Z轴也旋转90°而不会带动X轴旋转，此时Z轴就会和X轴重合，导致绕X、Z轴旋转的结果完全一样。

平衡环有这个前提条件是由于其机械结构，而我们在实现欧拉角变换的时候，为什么也要遵守这个规则呢？

首先明确一点：

这一点其实就是反直觉的，我们经常下意识地将欧拉角变换理解成，先绕X轴转动一定角度，再绕Y轴，Z轴旋转一定角度，物体的旋转会带动其局部坐标系一同旋转，绕Y轴旋转90°，Y轴会带动Z轴也旋转90°并且带动X轴旋转90°。而真实的欧拉角变换是，通过一个由矩阵相乘计算出的最终旋转矩阵直接对物体进行一个变换，也就是说欧拉角旋转是一步完成的一个变换。

当我们一旦规定绕三个正交轴旋转的先后循序，我们就确定了构成最终旋转矩阵的矩阵相乘顺序，而在矩阵乘法中没有交换律。

我们规定了三个矩阵的相乘顺序是XYZ，即为：X(0°) * Y(90°) * Z(0°)，由线性代数知识可知，左侧矩阵的变换会被应用到其右侧的所有矩阵，这也就是平衡环中大环会带动小环，而小环不能带动大环的数学解释，也是为什么众多解释万向死锁的文章都用平衡环演示的原因。

因此这个数学解释也就十分合理了。

万向死锁造成的问题

其实万向死锁之后，并不是这个物体就再也不能随心所欲的旋转了，而是如果想要旋转，就需要同时对三个轴都旋转，这就会导致其旋转的移动轨迹不在正交平面上，就会导致我们不期望的转动轨迹。

同过欧拉角实现的旋转动画，其每次只是应用一个变换，只是这个变换比上一帧应用的变换更近一步，产生了物体在转动的效果，也就是说，欧拉角旋转每次都是被作用在物体的初始状态上，这也可以进一步解释为什么上述案例中X轴会和Z轴重合，而不会随着物体转动而转动了，换个说法也就是在我们的直观理解中的新的X轴从来就不存在。

实际应用

由我们上述的分析可知万向节死锁不可避免，不论怎样安排绕三个正交轴的旋转顺序，其中间的轴一旦旋转90°或-90°，均会产生万向节死锁。

在实际运用中，一般会根据旋转的具体场景，将最不可能旋转到90°的轴安排在中间，比如在unity中，物体在Scene视图中的移动就是欧拉角移动，unity将x轴安排在中间，因为绕X轴的旋转即Pitch一般不会到达90°。

在Unity中使用Transform.Rotate实现欧拉的旋转。