代码随想录-数组

数组

二分查找

LeetCode.704

二分查找针对有序数组，每次能排除一半的元素，查找时间复杂度O(logN)；
二分查找代码编写时容易出错的是循环中止条件以及缩小区间时首位位置的确定，主要根据二分区间的左右开闭确定，建议使用左闭右闭区间，容易记忆。

核心代码：

int begin = 0;
int end = nums.size()-1;
while(begin <= end){  // [begin, end]，左闭右闭区间，左右边界可以相等
    int middle = (begin + end)/2;
    if(nums[middle]>target){
        end = middle-1;  // 搜索左半区间
    }else if(nums[middle]<target){
        begin = middle +1;  // 搜索右半区间
    }else{
        return middle;
    }
}

移除元素（快慢指针）（⭐）

LeetCode.27

这题考察的是对数组的元素删除，最暴力的思路是查找到要删除的元素，将其后的所有元素往前移一位并将数组长度减一，实现“删除”操作，这种算法时间复杂度为 O(N)。
还可以使用快慢指针的方法，很巧妙，快指针指向的元素覆盖慢指针指向的元素，但是当快指针指向要删除元素时，不赋值并且不递增慢指针（让慢指针指向要删除的元素）；

核心代码：

int len = nums.size();
int slow = 0;
for(int fast=0;fast<nums.size();fast++){
    if(nums[fast]!=val){
        nums[slow]=nums[fast];
        slow++;
        // nums[slow++]=nums[fast]; 后加加表示先取值进行运算再加
    }else{ // 当走到要删除的元素时，不赋值并让slow指向该位置，走到不是要删除元素时，就会覆盖当前slow指向的元素，并将数组长度减一
        len--;
    }
}
return len;

有序数组的平方（双指针）

LeetCode.977

此题暴力解法就是全平方再排序（快排），时间复杂度O(NlogN)；
还可以使用双指针的方法，因为有序数组中有负数，那么平方后的最大值一定是最小的负数或者最大的正数，因此用两个指针分别指向头尾，比较平方后的值再填入新数组即可；

核心代码：

int begin = 0;
int end = nums.size()-1;
vector<int> res(nums.size());
for(int i=end;i>=0;i--){
    int sqrt_begin = nums[begin]*nums[begin];
    int sqrt_end = nums[end]*nums[end];
    if(sqrt_begin>sqrt_end){
        res[i]=sqrt_begin;
        begin++;
    }else{
        res[i]=sqrt_end;
        end--;
    }
}
return res;

长度最小的子数组|滑动窗口（⭐⭐）

LeetCode.209

此题暴力法就是计算每个子数组的长度，时间复杂度为O(N^2)；
更好的方法是滑动窗口，一个for循环先向后遍历并记录当前sum值，当sum大于等于target时，记录当前子数组长度，之后开始移动慢指针缩小子数组长度，for循环遍历结束后即可得到最小的子数组长度；
时间复杂度为**O(N)**，虽然循环中还有一个循环，但是每个元素只被操作了两次（进滑动窗口时加到sum，出滑动窗口时从sum减去），共操作了2N次；

核心代码：

int sum = 0;
int slowPtr = 0;
int res = 0;
for(int i = 0;i<nums.size();i++){
    sum+=nums[i];
    while(sum>=target){   
        int subL = i-slowPtr+1;  // 记录当前子数组长度
        if(res==0){
            res = subL;
        }else{
            res = min(res, subL);
        }
        sum-=nums[slowPtr]; // 向后移动慢指针
        slowPtr++;
    }
}
return res;

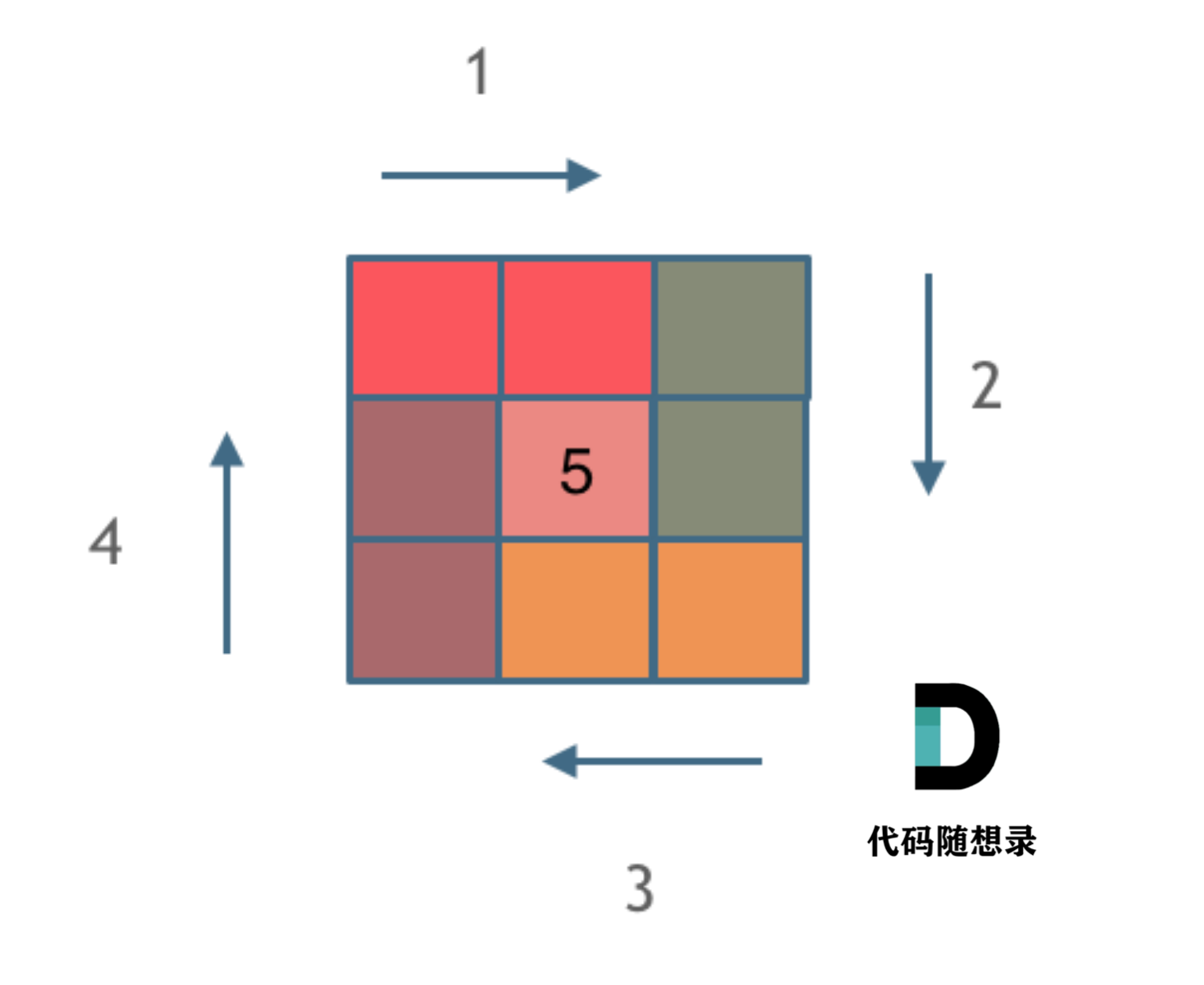
螺旋矩阵

LeetCode.59

此题为一道模拟题，没什么算法，主要要注意边界处理要一致（如上图所示）；

核心代码：

vector<vector<int>> res(n, vector<int>(n)); // 使用vector定义二维数组
int count = 1; 
int loop = n/2;
int mid = n/2;
int startx = 0, starty = 0;
int offset = 1;
int i, j;
while(loop>0){
    for(j=starty;j<n-offset;j++){ // 每一圈从startx，starty开始，offset控制尾部不处理
        res[startx][j]=count++; // 后加加，先赋值再加；
    }
    for(i=startx;i<n-offset;i++){
        res[i][j]=count++;
    }
    for(;j>starty;j--){
        res[i][j]=count++;
    }
    for(;i>startx;i--){
        res[i][j]=count++;
    }
    startx++;
    starty++;
    offset++;
    loop--;
}
if(n%2==1){
    res[mid][mid]=count;
}
return res;