代码随想录-二叉树

二叉树

二叉树的递归遍历（⭐⭐⭐）

写递归函数的思考逻辑：（⭐⭐⭐）

1. 确定递归函数的参数和返回值
2. 确定终止条件
3. 确定单层递归的逻辑

前序遍历：

void traversal(TreeNode* cur, vector<int>& res){
    if(cur==nullptr) return;
    res.push_back(cur->val);  // 中
    traversal(cur->left, res);  // 左
    traversal(cur->right, res);  // 右
}

中序遍历：

void traversal(TreeNode* cur, vector<int>& res){
    if(cur==nullptr) return;
    traversal(cur->left, res);  // 左
    res.push_back(cur->val);  // 中
    traversal(cur->right, res);  // 右
}

后序遍历：

void traversal(TreeNode* cur, vector<int>& res){
    if(cur==nullptr) return;
    traversal(cur->left, res);  // 左
    traversal(cur->right, res);  // 右
    res.push_back(cur->val);  // 中
}

二叉树的迭代遍历（非递归）（⭐⭐⭐）

前序遍历：

vector<int> preorderTraversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> stack;
    if(root==nullptr){
        return res;
    }
    stack.push(root);
    while(!stack.empty()){
        TreeNode* temp=stack.top();
        res.push_back(temp->val);
        stack.pop();
        // 先让右孩子入栈再让左孩子入栈，因为栈是先进后出
        if(temp->right!=nullptr){  // 右孩子不为空，入栈
            stack.push(temp->right);
        }
        if(temp->left!=nullptr){
            stack.push(temp->left);  // 左孩子不为空，入栈
        }
    }
    return res;
}

中序遍历：（⭐⭐⭐）

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> res;
    if(root==nullptr){
        return res;
    }
    stack<TreeNode*> stack;
    TreeNode* cur=root;
    while(cur!=nullptr||!stack.empty()){
        if(cur!=nullptr){
            stack.push(cur);
            cur=cur->left;  // 左
        }else{
            cur = stack.top();
            res.push_back(cur->val);  // 中
            stack.pop();
            cur=cur->right;  // 右
        }
    }
    return res;
}

后序遍历：
后序遍历的非递归算法有些技巧，不需要模拟后序遍历的递归栈；前序遍历顺序是 中左右，后序遍历顺序是 左右中，因此可以使用前序遍历顺序为中右左得到数组，再reverse数组即可。

vector<int> postorderTraversal(TreeNode* root) {
    vector<int> res;
    if(root==nullptr){
        return res;
    }
    stack<TreeNode*> stack;
    stack.push(root);
    while(!stack.empty()){
        TreeNode* tempNode=stack.top();
        stack.pop();
        res.push_back(tempNode->val);
        if(tempNode->left!=nullptr){
            stack.push(tempNode->left);
        }
        if(tempNode->right!=nullptr){
            stack.push(tempNode->right);
        }
    }
    reverse(res.begin(),res.end());
    return res;
}

二叉树的层序遍历（⭐⭐⭐）

二叉树的层序遍历（⭐⭐）

LeetCode.102

核心代码：

vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>> res;
    if(root==nullptr){
        return res;
    }
    queue<TreeNode*> queue;
    queue.push(root);
    while(!queue.empty()){
        int size=queue.size();  // 记录当前队列中元素个数，就是当前层的元素个数
        vector<int> secVec;
        for(int i=0;i<size;i++){
            TreeNode* tempNode=queue.front();
            queue.pop();
            secVec.push_back(tempNode->val);
            if(tempNode->left!=nullptr){
                queue.push(tempNode->left);
            }
            if(tempNode->right!=nullptr){
                queue.push(tempNode->right);
            }
        }
        res.push_back(secVec);
    }
    return res;
}

二叉树的层序遍历Ⅱ

LeetCode.107

和上一题一样，最后翻转结果数组即可；

核心代码：

vector<vector<int>> levelOrderBottom(TreeNode* root) {
    vector<vector<int>> res;
    if(root==nullptr){
        return res;
    }
    queue<TreeNode*> queue;
    queue.push(root);
    while(!queue.empty()){
        int size=queue.size();
        vector<int> secVec;
        for(int i=0;i<size;i++){
            TreeNode* tempNode=queue.front();
            secVec.push_back(tempNode->val);
            queue.pop();
            if(tempNode->left!=nullptr){
                queue.push(tempNode->left);
            }
            if(tempNode->right!=nullptr){
                queue.push(tempNode->right);
            }
        }
        res.push_back(secVec);
    }
    reverse(res.begin(),res.end());
    return res;
}

二叉树的右视图

LeetCode.199

核心代码：

while(!queue.empt()){
    int size=queue.size();
    for(int i=0;i<size;i++){
        //...
        if(i==size-1){
            res.push_back(tempNode->val);
        }
    }
}

二叉树的层平均值

LeetCode.637

核心代码：

while(!queue.empt()){
    int size=queue.size();
    double sum=0
    for(int i=0;i<size;i++){
        //...
        sum+=tempNode->val;
    }
    res.push_back(sum/size);
}

N叉树的层序遍历

LeetCode.429

核心代码：

while(!queue.empt()){
    int size=queue.size();
    for(int i=0;i<size;i++){
        //...
        res.push_back(node->val);
        for(int i=0;i<node->children.size();i++){
            if(node->children[i]!=nullptr){
                queue.push(node->children[i]);
            }
        }
    }
}

在每个树行中找最大值

LeetCode.515

记录最大值即可。

翻转二叉树

LeetCode.226

核心代码：

// 迭代法
void invert(TreeNode* root){
    if(root==nullptr) return;
    swap(root->right, root->left);
    invert(root->left);
    invert(root->right); 
}
TreeNode* invertTree(TreeNode* root){
    invert(root);
    return root;
}
// 递归法
TreeNode* invertTree(TreeNode* root) {
    if(root==nullptr){
        return root;
    }
    stack<TreeNode*> stack;
    stack.push(root);
    while(!stack.empty()){
        TreeNode* node=stack.top();
        stack.pop();
        swap(node->left, node->right);
        if(node->left){
            stack.push(node->left);
        }
        if(node->right){
            stack.push(node->right);
        }
    }
    return root;
}

对称二叉树（⭐）

LeetCode.101

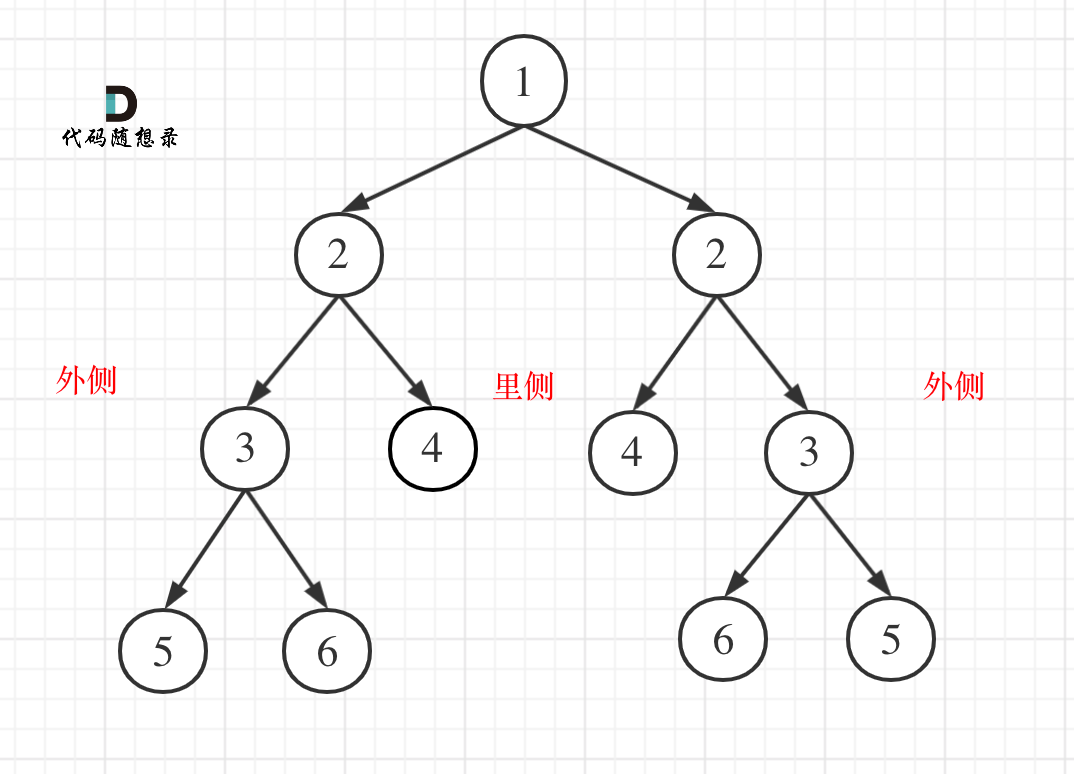
核心代码：

// 递归法（⭐⭐）
bool compare(TreeNode* leftNode, TreeNode* rightNode){
    if(!leftNode&&rightNode){
        return false;
    }else if(leftNode&&!rightNode){
        return false;
    }else if(!leftNode&&!rightNode){
        return true;
    }else if(leftNode->val!=rightNode->val){
        return false;
    }
    bool outside=compare(leftNode->left, rightNode->right);
    bool inside=compare(leftNode->right, rightNode->left);
    return outside&&inside;
}
bool isSymmetric(TreeNode* root) {
    return compare(root->left, root->right);
}
// 使用栈迭代法
bool isSymmetric(TreeNode* root) {
    stack<TreeNode*> st;
    st.push(root->left);
    st.push(root->right);
    while(!st.empty()){
        TreeNode* rightNode=st.top();
        st.pop();
        TreeNode* leftNode=st.top();
        st.pop();
        if(!rightNode&&!leftNode){
            continue;
        }
        if((!rightNode||!leftNode||(rightNode->val!=leftNode->val))){
            return false;
        }
        st.push(leftNode->left);
        st.push(rightNode->right);
        st.push(leftNode->right);
        st.push(rightNode->left);
    }
    return true;
}

二叉树的最大深度

LeetCode.104

核心代码：

// 递归法
int func(TreeNode* root){
    if(root==nullptr){
        return 0;
    }
    int leftDepth=func(root->left);
    int rightDepth=func(root->right);
    return max(leftDepth, rightDepth) + 1;
}
int maxDepth(TreeNode* root) {
    if(root==nullptr){
        return 0;
    }
    return func(root);
}
// 层序遍历
int maxDepth(TreeNode* root) {
    if(root==nullptr) return 0;
    int res=0;
    queue<TreeNode*> que;
    que.push(root);
    while(!que.empty()){
        int size = que.size();
        for(int i=0;i<size;i++){
            TreeNode* node=que.front();
            que.pop();
            if(node->left) que.push(node->left);
            if(node->right) que.push(node->right);
        }
        res+=1;
    }
    return res;
}

二叉树的最小深度（⭐）

LeetCode.111

本题递归法和求二叉树最大深度类似，只是要处理没有子树的情况，如一个树只有右子树，他的最小深度不是1；
本题迭代法使用层序遍历，当一个节点没有左右儿子时说明其是叶子节点，故第一次遇到没有左右儿子的节点时就是最小深度；

// 递归法
int minDepth(TreeNode* root) {
    if(root==nullptr) return 0;
    int depth=0;
    int leftDepth=minDepth(root->left);
    int rightDepth=minDepth(root->right);
    if(leftDepth!=0&&rightDepth!=0){
        depth = min(leftDepth, rightDepth);
    }else if(leftDepth==0){
        depth=rightDepth;
    }else{
        depth=leftDepth;
    }
    return depth+1;
}
// 层序遍历迭代法
int minDepth(TreeNode* root) {
    if (root == nullptr)
        return 0;
    int depth = 0;
    queue<TreeNode*> que;
    que.push(root);
    while (!que.empty()) {
        int size = que.size();
        depth++;
        for (int i = 0; i < size; i++) {
            TreeNode* node = que.front();
            que.pop();
            if (node->left)
                que.push(node->left);
            if (node->right)
                que.push(node->right);
            if (!node->left && !node->right) { // 没有左右孩子，说明是叶子节点，遇到叶子节点直接返回当前深度
                return depth;
            }
        }
    }
    return depth;
}

完全二叉树的节点个数

本题直接求个数了，没用到完全二叉树的性质；

平衡二叉树（⭐）

LeetCode.110

核心代码：

int getHeight(TreeNode* root){
    if(root==nullptr){
        return 0;
    }
    int leftHeight=getHeight(root->left);
    int rightHeight=getHeight(root->right);
    if(leftHeight==-1||rightHeight==-1){
        return -1;
    }
    if(abs(leftHeight-rightHeight)<=1){
        return max(leftHeight, rightHeight)+1;
    }else{
        return -1;
    }
}
bool isBalanced(TreeNode* root){
    if(root==nullptr) return true;
    if(getHeight(root)!=-1){
        return true;
    }else{
        return false;
    }
}

二叉树的所有路径（⭐）

LeetCode.257

关键在于理解二叉树的遍历；

核心代码：

vector<string> binaryTreePaths(TreeNode* root){
    vector<string> res;
    stack<TreeNode*> treeSt;
    stack<string> pathSt;
    treeSt.push(root);
    pathSt.push(to_string(root));
    while(!treeSt.empty()){
        TreeNode* node=treeSt.top(); treeSt.pop();
        string path=pathSt.top(); pathSt.pop();
        if(!node->left&&!node->right){
            res.push_back(path);
        }
        if(node->right){
            treeSt.push(node->right);
            pathSt.push(path+"->"+to_string(node->right->val));
        }
        if(node->left){
            treeSt.push(node->left);
            pathSt.push(path+"->"+to_string(node->left->val));
        }
    }
    return res;
}